如何看懂这些代码的意思?以及代码后面的公式
挂出这一篇文章吧 拓扑优化 ,估计毕业了更没时间写...
原答案:
等我毕业了来答
有一个北理工学生的拓扑优化学习报告可供参考:
拓扑优化学习报告_北理工_王路_百度文库这个报告将99行代码中涉及到的力学概念和拓扑优化方法都基本讲解了,而且写得挺清楚的,很适合初学者去看。
最近在搞拓扑优化,导师给了mmc中提到了Sigmund的99行代码,花费了好久才啃完这篇,万事开头难。
我把每一行代码都注释了,还有自己的理解,希望给大家提供一些帮助。
水平有限,如有错误请见谅,仅代表个人意见。
如有转载请联系我,因为可能有错的,家丑不能外扬。如果有什么问题不懂,或者有什么地方我说错了,也可以私信我。
总是有人给我点赞,搞得我有点慌,于2021.9.24再次修订,补充纠正了一些内容。
有一些错误,随着学习的不断深入才意识到,于2022年11月15日再次修订。
%%%% A 99 LINE TOPOLOGY OPTIMIZATION CODE BY OLE SIGMUND, JANUARY 2000 %%%
%%%% CODE MODIFIED FOR INCREASED SPEED, September 2002, BY OLE SIGMUND %%%
function top(nelx,nely,volfrac,penal,rmin);
% INITIALIZE
x(1:nely,1:nelx) = volfrac; %全局给一个初始体积分数
loop = 0; %累计一共迭代循环了几次
change = 1.;%该变量,用来判断变化量,如果小于某一个值就终止
% START ITERATION
while change > 0.01 %改变大于0.01跳出循环,否则执行
loop = loop + 1;%每次循环会累计1,也可以通过迭代多少次来决定程序的终止,而不仅仅是change
xold = x;%x的old等于上一次循环的结果,用来和当前x相比较进而计算change
% FE-ANALYSIS
[U]=FE(nelx,nely,x,penal); %根据单元数目和上次循环得到的x,通过f=ku来计算u,详见子函数
% OBJECTIVE FUNCTION AND SENSITIVITY ANALYSIS
[KE] = lk;%这里得到单元的ke矩阵,详见子函数(往下翻,在最后)
c = 0.;%用来叠加,先初始化为0,这是目标函数
for ely = 1:nely%y方向迭代
for elx = 1:nelx%x方向对每个单元迭代,xy两个方向就是对所有单元进行循环同一种操作
n1 = (nely+1)*(elx-1)+ely; %指单元的左上角自由度
n2 = (nely+1)* elx +ely; %每个单元的右上角自由度
%这里的编号,是从左到右,从上到下,比如最左上角为1,往下2,3,直到该列结束
Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1);%这里是单元节点各自由度的编号
%对这里单元自由度编号不太明白的可以往下翻,我后面有进一步的解释,这里给各个自由度进行编号方便刚度阵的组装
c = c + x(ely,elx)^penal*Ue'*KE*Ue;%通过每个单元的目标函数叠加得到总体的目标函数值,
%目标函数就是所有单元的柔度值,柔度就是FU,其中F=KU,所以总体来说矩阵形式就是UKU
%一般来说大家都是以柔度作为目标函数,是因为C=FU,F固定的情况下,结构肯定位移U越少越好;U固定的情况下
%力F越小越好,这样结构应力小,所以用Fu的乘积能够比较好的衡量结构的刚度特性
%c是指compliance
%这里目标函数指柔度c=fu
dc(ely,elx) = -penal*x(ely,elx)^(penal-1)*Ue'*KE*Ue;%进行灵敏度分析,其实就是c对x求导,得到每x变化引起的c变化
%也就是顾名思义的灵敏度,具体文献里面有推导得到最后的公式
end
end
% FILTERING OF SENSITIVITIES
[dc] = check(nelx,nely,rmin,x,dc); %检查灵敏度,把一开始的dc输入进行加权修正,防止棋盘格现象,具体参见后面子函数
% DESIGN UPDATE BY THE OPTIMALITY CRITERIA METHOD%利用优化准则更新变量
[x] = OC(nelx,nely,x,volfrac,dc); %这一步是更新的关键部分,是这一部分让x朝着想要的方向更新,具体也参见后面子函数
%这里x指xnew,省略new做连接,和xold,实现迭代
%不动点迭代法
% PRINT RESULTS
change = max(max(abs(x-xold)));%正如上文提到的xold,这里当前迭代中的x和之前一步的xold比较得到变化
%如果结构基本没变化了,就可以认为迭代基本收敛了
disp([' It.: ' sprintf('%4i',loop) ' Obj.: ' sprintf('%10.4f',c) ...%打印迭代的步数和目标函数
' Vol.: ' sprintf('%6.3f',sum(sum(x))/(nelx*nely)) ...%打印体积分数,sum加两次分别是行列相加
' ch.: ' sprintf('%6.3f',change )])%打印每次更新后该变量的变化
% PLOT DENSITIES
colormap(gray); imagesc(-x); axis equal; axis tight; axis off;pause(1e-6);%这里画图,里面存在四种函数用法
%colormap imagesc axis pause
%colormap查看并设置当前颜色图,gray是灰度图,只有黑白两色,0-1之间灰度变化,也有winter(主要是蓝色,冷色系),summer等色系,
%显示成灰度感觉最清晰
%imagesc,imagesc(C) 将数组 C 中的数据显示为一个图像,该图像使用颜色图中的全部颜色。C 的每个元素指定图像的一个像素的颜色。
%生成的图像是一个 m×n 像素网格,其中 m 和 n 分别是 C 中的行数和列数。这些元素的行索引和列索引确定了对应像素的中心。
%举个例子,比如0,1,2,4,7.则颜色由黑到白(gray)分为7份,7为黑,0为白,1 2 4对应相应的灰度程度按比例
%axis指坐标轴
%pause(n) 暂停执行 n 秒,然后继续执行。必须启用暂停,此调用才能生效。
%只有暂停了,图像才能显示出来
end
%%%%%%%%%% OPTIMALITY CRITERIA UPDATE %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [xnew]=OC(nelx,nely,x,volfrac,dc) %xnew是更新后的x,xold在程序初始已经储存了,需要参数dc和volfrac
l1 = 0; l2 = 100000; move = 0.2;%利用二分法来逼近l1 l2边界
%这里我个人理解为类似于二分法,也不知道对不对,暂且这样理解吧
while (l2-l1 > 1e-4)%边界距离小于这个值时终止循环
lmid = 0.5*(l2+l1);%边界中间值
xnew = max(0.001,max(x-move,min(1.,min(x+move,x.*sqrt(-dchttps://www.zhihu.com/question/lmid)))));%这里注意limd在分母上,下文有描述
%这个函数套的很复杂,理解了好久才理解过来。从内看会看懵逼,试着从外往内看就柳暗花明又一村
%这个大小依次时这种情况,0.001 x-move xbnu x+move 1,如果满足这个大小顺序,就取xbnu(不明白这个字母符号代表什么公式的请看论文原文,有具体形式)
%0.001是最小密度下限,毕竟不能取负值,所以要大于这个值,故max(0.001,)
%x-move是密度变化下限,每次不能变化太多,所以max(m-move,)
%1是上限,毕竟密度不能超过单位1,所以min(,1),这个满足了别急,还有一个上限
%x+move是变化的上限,所以min(,x+move)
%一切都是在判断xbnu的值,让它处在x-move 和 x+move之间,否则取上下限
%之所以这样做一方面是防止密度变成负值,或者变成大于1的值(0无材料,1实体材料,0-1中间材料,超过该范围就没意义了)
%而x-move and x+move should be included in[0.001,1],因为有x比较小的情况,这时再-0.2,比如x-move=0.13-0.2=负值
%负值就不行了,哪有密度是负的,所以取0.001,1也是同理
if sum(sum(xnew)) - volfrac*nelx*nely > 0%最后判断体积,如果大于给定的体积分数,就取下限为中间值,整个区间往上逼近
%意思就是limd变大,而limd在分母上,整个体积就会忘变小的方向移动
%否则小于给定的体积分数往下逼近
%意思就是如果体积小了,就增加体积,如果大,就减少
l1 = lmid;
else
l2 = lmid;
end
end
%%%%%%%%%% MESH-INDEPENDENCY FILTER %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [dcn]=check(nelx,nely,rmin,x,dc)%网格独立性过滤器,其实就是检查灵敏度
%对过滤半径以内的其他单元的敏度 进行加权平均,修正单元的灵敏度,从而避免棋盘格现象,
%通常能够减少棋盘格现象的方法都能减少网格依赖性。
dcn=zeros(nely,nelx);%先建立一个全部是0的用来待会存放的矩阵,用来存放灵敏度
%存放后方便使用sum符号,要进行累加来套公式
%提前规定好变量的空间,能提升效率
for i = 1:nelx
for j = 1:nely%对每一个单元进行循环
sum=0.0; %初始化总和
for k = max(i-floor(rmin),1):min(i+floor(rmin),nelx)%这两行表示,如果在圆的范围内,就要参与灵敏度修正
%这里的
%max(i-floor(rmin),1)是为了防止超过边界,如果超过边界变成负值,就按1处理,min同理,
%floor用来修正为整数
for l = max(j-floor(rmin),1):min(j+floor(rmin),nely)%注意i,j是目前所在的单元,k,l是距离中心的距离。
fac = rmin-sqrt((i-k)^2+(j-l)^2);%套公式,计算其中的卷积算子,一个用来表示权重的算子H
sum = sum+max(0,fac);%用来表示权重则只有正值,若负值则看成0,累加形成sum的效果sum(H),
%理解上max无视,直接当成fac看就行
dcn(j,i) = dcn(j,i) + max(0,fac)*x(l,k)*dc(l,k);%这里累加形成分子,sum(H*x*dc/dx)
end
end
dcn(j,i) = dcn(j,i)/(x(j,i)*sum);%这里将分子除以分母
%Sigmund 提出的敏度过滤技术的本质是利用过滤范围内所有单元的敏度 信息修正中心单元的敏度信息,这里修正的思想不是太理解
%大概就是采用过滤半径范围内各单元敏度的加权平均值代替中心单元的敏度值
%为什么这种方法有效呢,你想想,其实棋盘格就是相邻两个单元一个想减少,一个想增大,我一加权,考虑局部整体
%变化就趋向于一致,就抑制了棋盘格
end
end
%%%%%%%%%% FE-ANALYSIS %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [U]=FE(nelx,nely,x,penal)%这里是一个有限元程序,里面储存了边界信息
[KE] = lk; %引入ke
K = sparse(2*(nelx+1)*(nely+1), 2*(nelx+1)*(nely+1));%use "sparse" to save the memory maybe.
%here 2(nely+!)(+1)means
%每个节点有两个方向的k,就像是水平和竖直的弹簧,不知道这样理解对不对
%如果以后用得到,再具体复习有限元这一部分内容
%第二个2(nely+!)(+1)意思是其它节点对该结点处的影响,任何一个都可能在该处叠加,所以又一个2(nely+!)(+1),矩阵维数很大
F = sparse(2*(nely+1)*(nelx+1),1); U = zeros(2*(nely+1)*(nelx+1),1);%一个单元有四个节点,每个节点有两个方向的力和位移
%一个水平一个竖直
%(nely+1)(nelx+1)为一共节点数量,*2 means one point have f or u in two direction
for elx = 1:nelx
for ely = 1:nely%再次对单元循环
n1 = (nely+1)*(elx-1)+ely; %定义一个单元上左坐标为n1,右上坐标为n2
n2 = (nely+1)* elx +ely;%先横向,再竖向,横向2n1-1,竖向2n1,按竖向增加,节点单元都是这样
%故左下为2n1+1 2n1+2
%用n1 n2可以简化下面代码,不然看起来太长
edof = [2*n1-1; 2*n1; 2*n2-1; 2*n2; 2*n2+1; 2*n2+2; 2*n1+1; 2*n1+2];%这里以左上为起点,顺时针排列,感觉应该不影响
%顺时针逆时针都一样,数值不变,都是对应的
K(edof,edof) = K(edof,edof) + x(ely,elx)^penal*KE;%在对应位置处累加,注意这里edof中位
%置不一定相邻,这里是在对单元的刚度矩阵,对号放入到总体的刚度矩阵中
end
end
% DEFINE LOADS AND SUPPORTS (HALF MBB-BEAM)
F(2,1) = -1;%没错,这个力加在左上角,2是偶数,表示y方向,-1表示向下,施加单位力,具体图见Sigmund文献资料
fixeddofs = union([1:2:2*(nely+1)],[2*(nelx+1)*(nely+1)]);%这里的union按从小到大返回并集有待商讨,
%经过我的研究,这个并集没别的意思,单纯并起来,写一起也行,这样写比较清晰
%表示左边界x固定,右下角y固定
alldofs = [1:2*(nely+1)*(nelx+1)];%列举所有的自由度
freedofs = setdiff(alldofs,fixeddofs);%除去固定自由度,剩下的完全自由的节点自由度
% SOLVING
U(freedofs,:) = K(freedofs,freedofs) \\ F(freedofs,:);%求解自由的自由度,有限元中已经练习过,可以整体拿掉某行某列进行计算
U(fixeddofs,:)= 0;%固定处的位移为0
%%%%%%%%%% ELEMENT STIFFNESS MATRIX %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[KE]=lk%这里就是储存了一个ke的信息,这里采用了四节点的有限元单元,不过多注释,详见有限元
E = 1.;
nu = 0.3;
k=[ 1/2-nu/6 1/8+nu/8 -1/4-nu/12 -1/8+3*nu/8 ...
-1/4+nu/12 -1/8-nu/8 nu/6 1/8-3*nu/8];
KE = E/(1-nu^2)*[ k(1) k(2) k(3) k(4) k(5) k(6) k(7) k(8)%直接套公式就行
k(2) k(1) k(8) k(7) k(6) k(5) k(4) k(3)
k(3) k(8) k(1) k(6) k(7) k(4) k(5) k(2)
k(4) k(7) k(6) k(1) k(8) k(3) k(2) k(5)
k(5) k(6) k(7) k(8) k(1) k(2) k(3) k(4)
k(6) k(5) k(4) k(3) k(2) k(1) k(8) k(7)
k(7) k(4) k(5) k(2) k(3) k(8) k(1) k(6)
k(8) k(3) k(2) k(5) k(4) k(7) k(6) k(1)];
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% This Matlab code was written by Ole Sigmund, Department of Solid %
% Mechanics, Technical University of Denmark, DK-2800 Lyngby, Denmark. %
% Please sent your comments to the author: sigmund@fam.dtu.dk %
% %
% The code is intended for educational purposes and theoretical details %
% are discussed in the paper %
% "A 99 line topology optimization code written in Matlab" %
% by Ole Sigmund (2001), Structural and Multidisciplinary Optimization, %
% Vol 21, pp. 120--127. %
% %
% The code as well as a postscript version of the paper can be %
% downloaded from the web-site: http://www.topopt.dtu.dk %
% %
% Disclaimer: %
% The author reserves all rights but does not guaranty that the code is %
% free from errors. Furthermore, he shall not be liable in any event %
% caused by the use of the program. %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%这里只是给出了代码的整体逻辑,个中公式模型的选择,个中原理,详细参考文献。推荐学习变密度法,还有有限元内容也需要具体学习,当然matlab需要学习就不说了。(才发现不知不觉已经打了这么多基础)
那个 emmm Sigmund的一些可以多读读 论文啊 综述啊 书啊
我只是一个大四的小萌新 太复杂的问题我回答不上来 好多大佬找我我有点慌了 饶在下一命
2020.11.15补充
这里推荐一个人(Haotian_W)写的博客,我感觉很好。
其中 包括99行和88行的解读。简单说一下,88行和99行的效率优化版
其中88行:TopOpt | 针对99行改进的88行拓扑优化程序完全注释
其中99行:TopOpt | 99行拓扑优化程序完全注释
2021/4/14根据大家私信我的一些问题和评论区的一些问题进行回答补充。
一、有人问如何更改设计域
关于评论区问如何从矩形变为L型,我觉得这个问题描述不是特别准确,应该是如何把设计域的形状改变为L型,而不是单元形状,单元还是矩形比较方便,也有用三角形的。因为很多文献会把L型作为算例之一。如图:
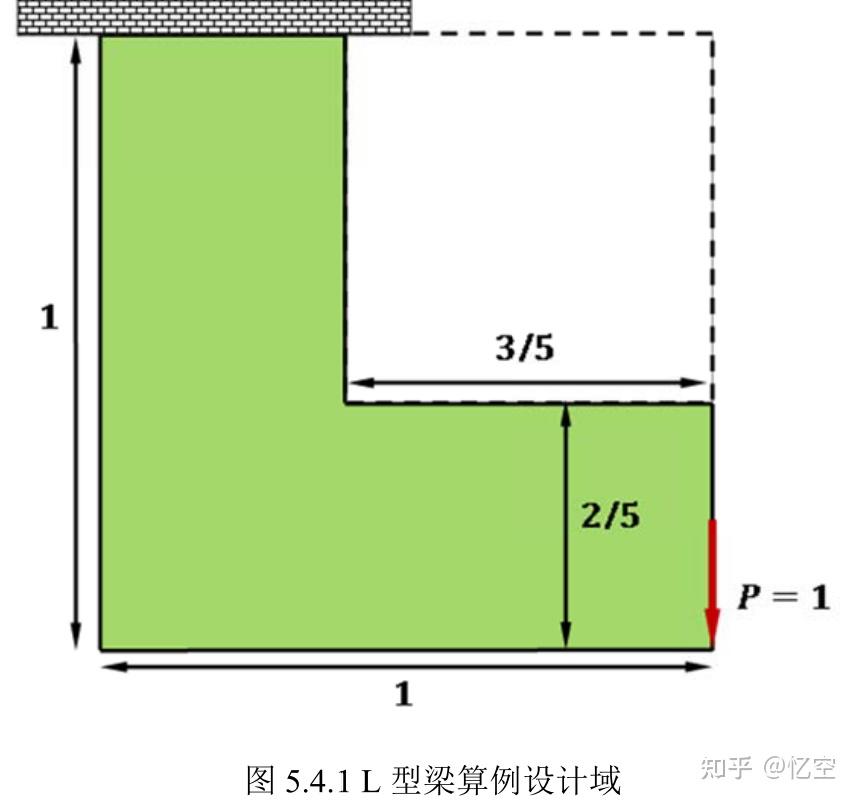
首先,我想说,99行变密度法论文里面说的很清楚,我也提到了这是基础知识,也提到了这篇论文,还是推荐好好读一下,提高独自解决问题的能力。如图,取自99行论文:

方法就是把你不需要的部分设计域,将其设计变量定义为0.代码可以这样写:

这里还有另外一种方法:把不需要的地方,用固定边界围起来。不过我没试过。
二、还有人问我matlab的数据结构
如图,不想打字了,名字已匿。
可以自己设计一个简单的matlab算例进行观察,语言表述终究没有自己实践感悟来的清楚。就相当于坐标处的坐标值。
三、还有人问如何确定整个模型中的某个位置的坐标表达方法
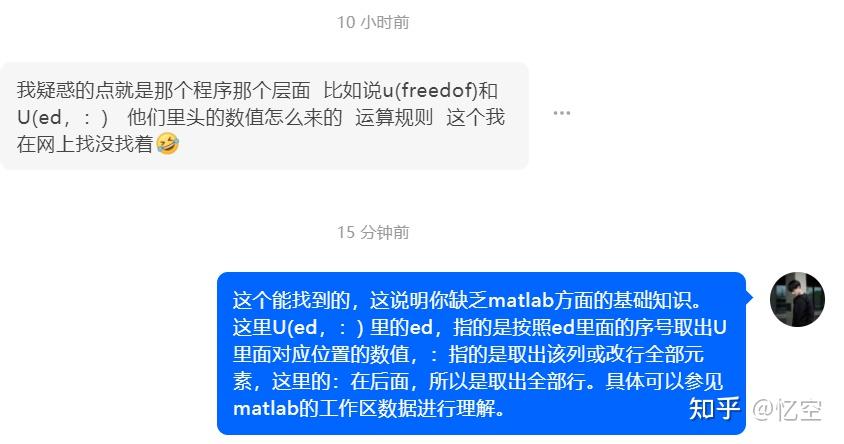
这里对所有单元都进行了编号,节点也进行了编号,节点自由度也进行了编号。我们可以通过这个编号来找到对应的位置。这个我给出的后面的别人博客里也有更进一步的解释,还是推荐看一下:
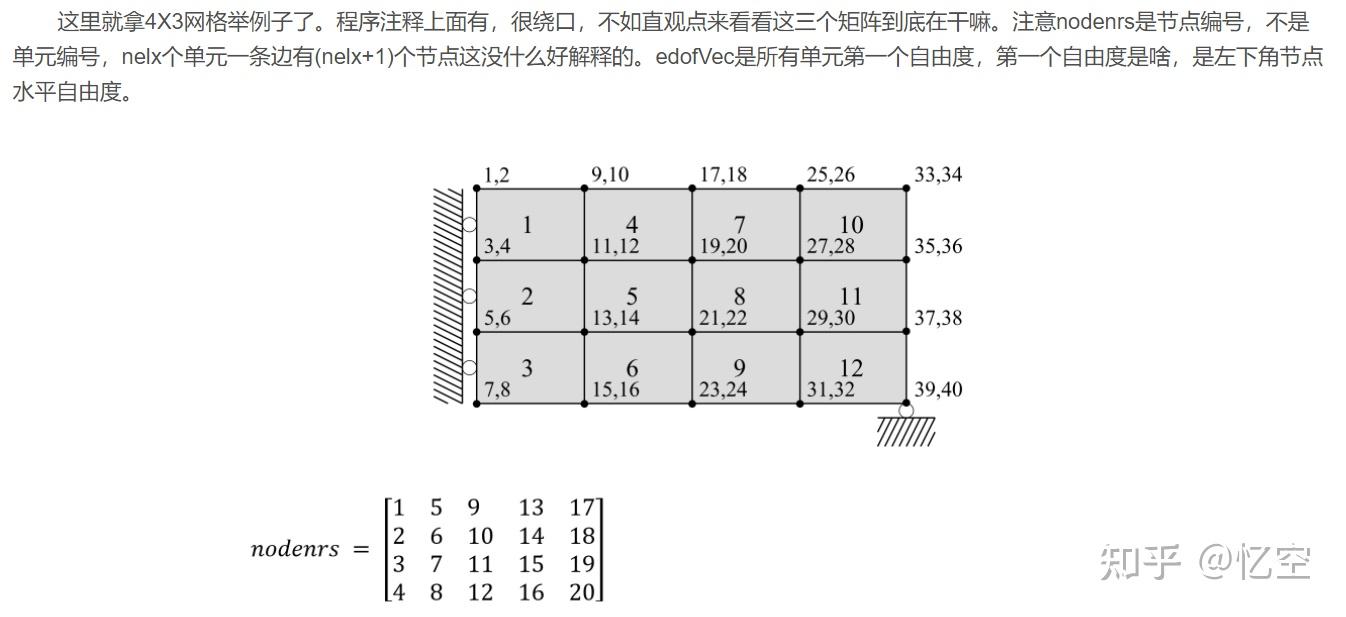
三、其它补充说明
关于多工况,其实就是分别求出每种工况的各自的目标函数,灵敏度,最后加起来,如此优化即可。
关于热应力,其实就是灵敏度里面多了一项因为热变形引起的热载荷向量的导数而已,如此。
Hypermesh结构优化设计基于数学最优化理论为基础,并建立响应条件,在满足约束的情况下,寻找最优的设计方案。在Hypermesh有限元网格中,可在analysis操作面板中点击Optimization,可以找到多种不同的优化手段。本文首先介绍自由尺寸优化(
):设计变量为壳单元,设计各个壳单元的厚度,从而得出结构的最优化厚度。建立几何模型,并划分网格单元尺寸为2的网格;在四周顶点进行固定端约束,分别在孔位中心处施加大小为5,方向为Z轴负向的载荷,如下图所示:
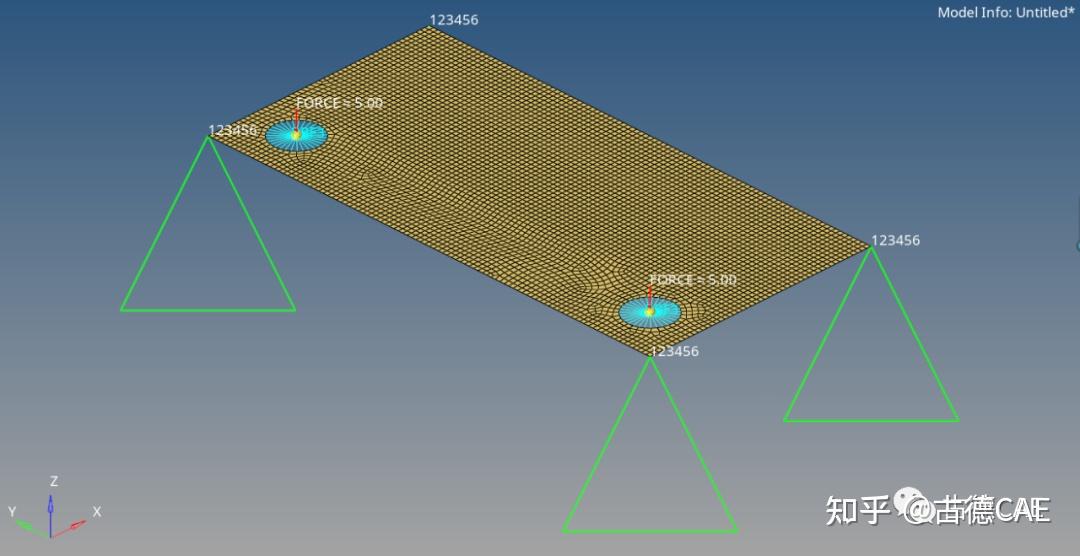
采用PLY铺层的方法建立有限元模型,参考前文方法“基于PLY的层合板建模”材料选择碳纤维复合材料,单层厚度为0.2mm,共铺设5层,铺层角度为[0°/45°]S。建立名为Freesize的设计变量,在type下选择stack,并在prop中选择上文建立的laminates,点击creat按钮,如下图所示:

进入下方composites面板,点击右下方edit面板进行设置;在PLYTHK建立最小单元厚度0.18mm,最大单元厚度0.25mm,PLYPCT可设置铺层比例约束,均衡制造约束BALANCE等,点击return,完成创建,如下图所示:
在response面板分别创建体积分数响应volumefrac和柔度响应compliance,在dconstraints面板中创建制造约束,体积分数不大于35%,点击creat,完成创建,并返回上一级面板,如下图所示:

在objective中,选择最小化柔度为优化设计目标,并选择静力学分析为基础的优化设计,如下图所示:

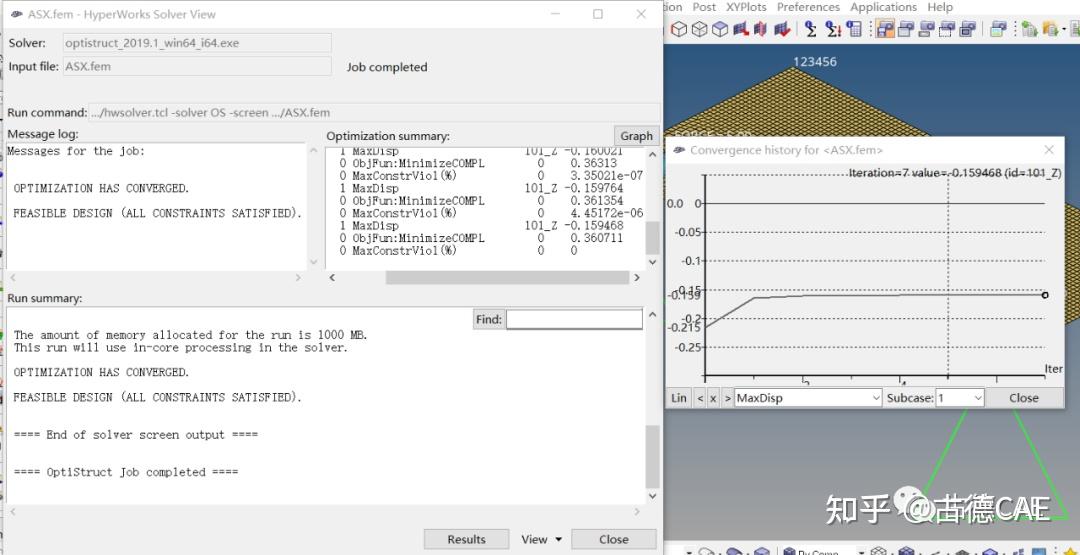
最终在解算面板中,将analysis切换为optimization优化,并计算最终结果。本文所示模型经过7次优化后完成优化设计,最终结果如下图所示。
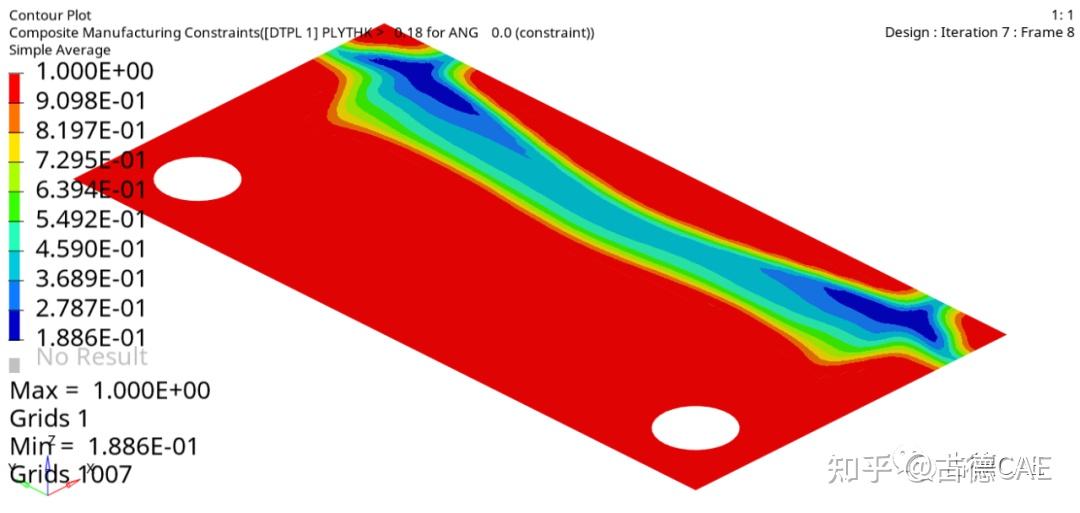
文章内容均为原创,侵权必究!!!